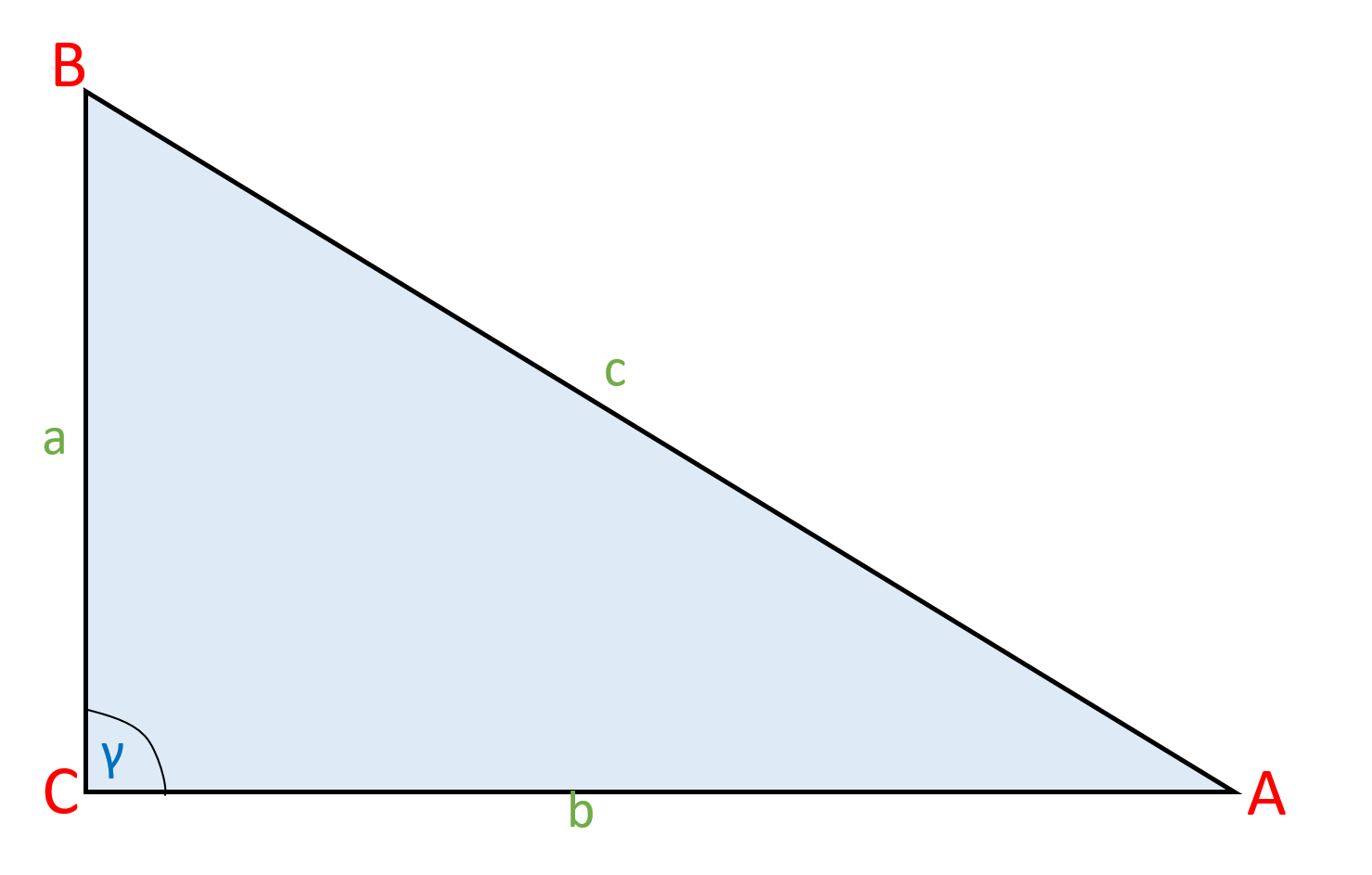
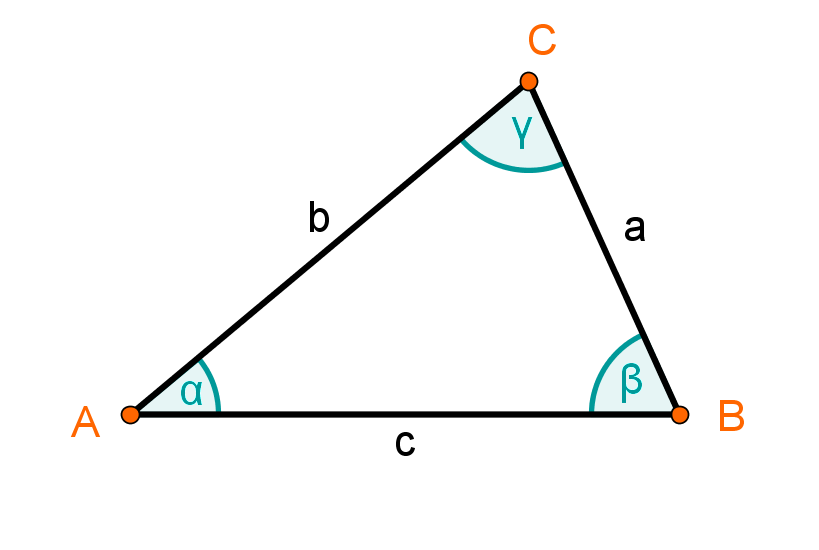
Das stumpfwinklige Dreieck setzt sich aus einem Winkel zwischen 90 und 180 Grad und zwei spitzen Winkeln unter 90 Grad zusammen. Wie groß die jeweiligen Winkel eines Dreiecks sind, lässt sich nur bedingt ohne Berechnung bestimmen. Als Dreieck gilt alles, was durch drei Seiten miteinander verbunden ist und eine messbare Innenfläche bietet.. Die Außenwinkel in einem Dreieck werden mit α’, β’ und γ’ beschriftet. Innen- und Außenwinkel ergeben zusammen immer 180°. Gleichzeitig ist ein Außenwinkel so groß wie die beiden gegenüberliegenden Winkel zusammen . 45° 45° 90° 135° a b. Ein Dreieck besteht aus drei Innenwinkeln und deren Größe bestimmt die Art des Dreiecks.
Dreieck berechnen Jetzt die Formeln & ihre Anwendung verstehen!

M9 Aufgaben zur Trigonometrie am rechtwinkligen Dreieck RSGWiki

Dreiecke nach Winkel klassifizieren YouTube

Das Dreieck und seine Winkel YouTube

Wie viel Grad hat ein Dreieck? Ein mathematisches Rätsel gelöst
Dreieck lernen mit Serlo!
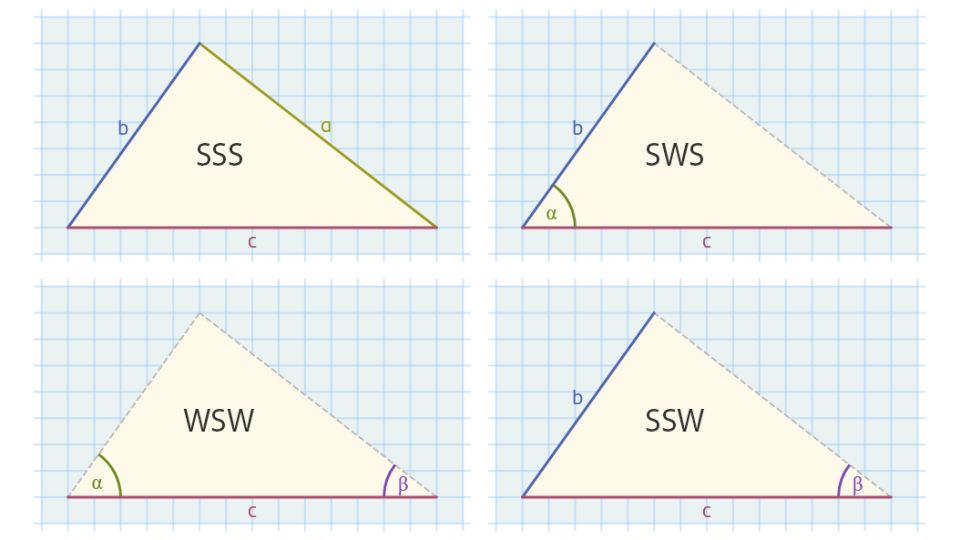
Dreiecke konstruieren Mathematik SchuBu
Dreiecke Grundlagen einfach online erklärt sofatutor
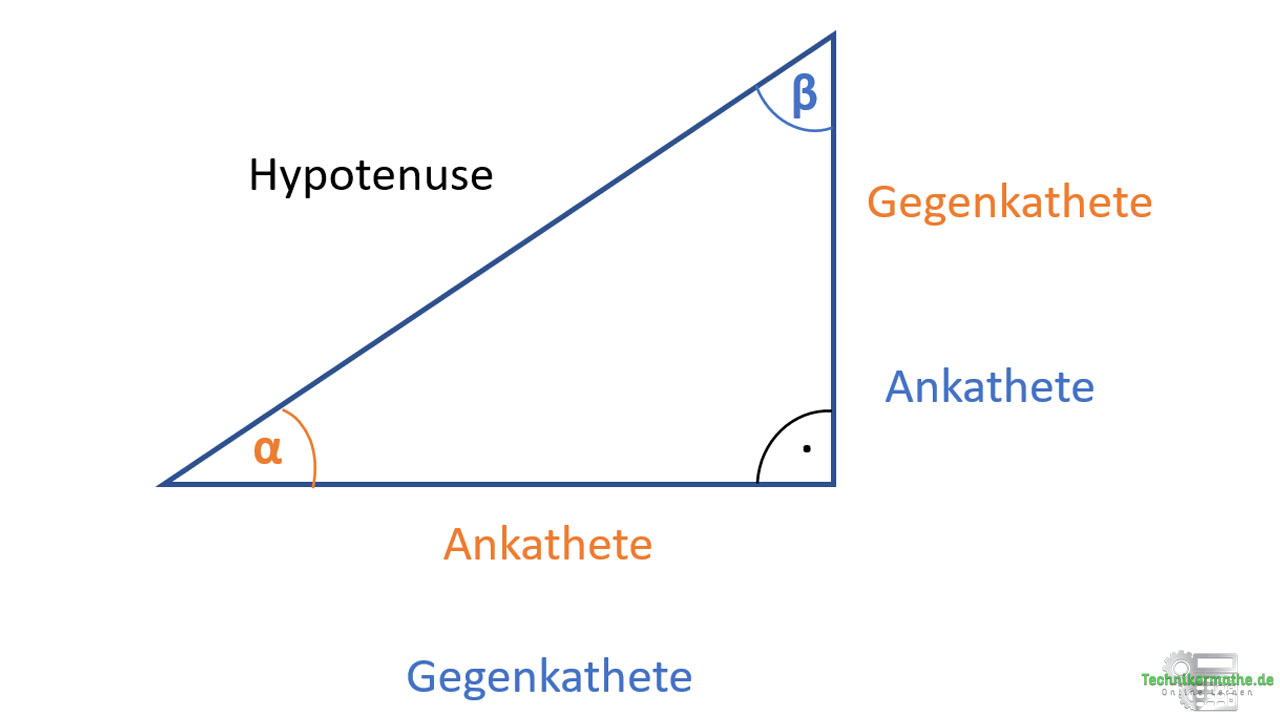
Trigonometrie am rechtwinkligen Dreieck 1a Technikermathe.de
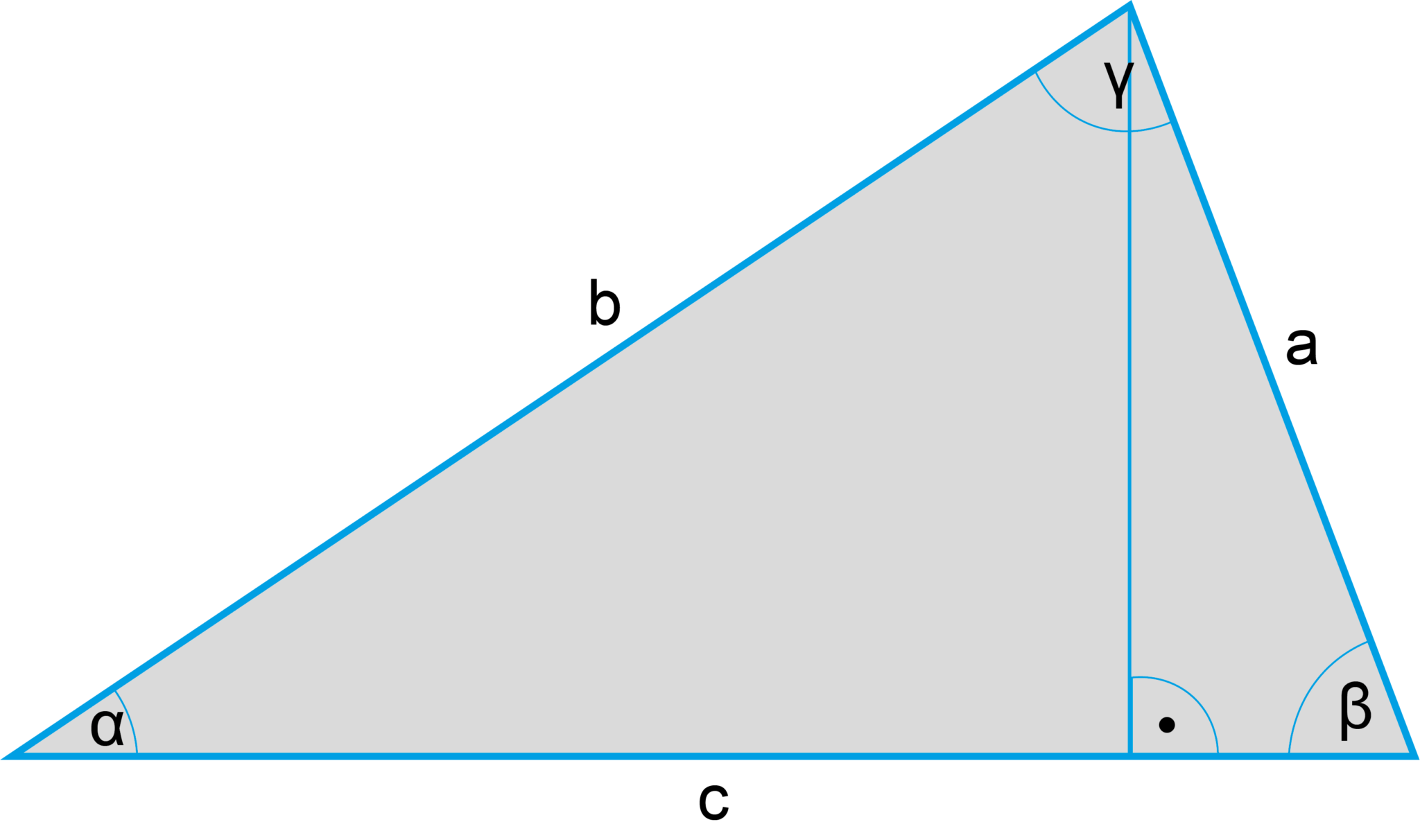
Flächeninhalt berechnen geometrische Figuren verstehen!
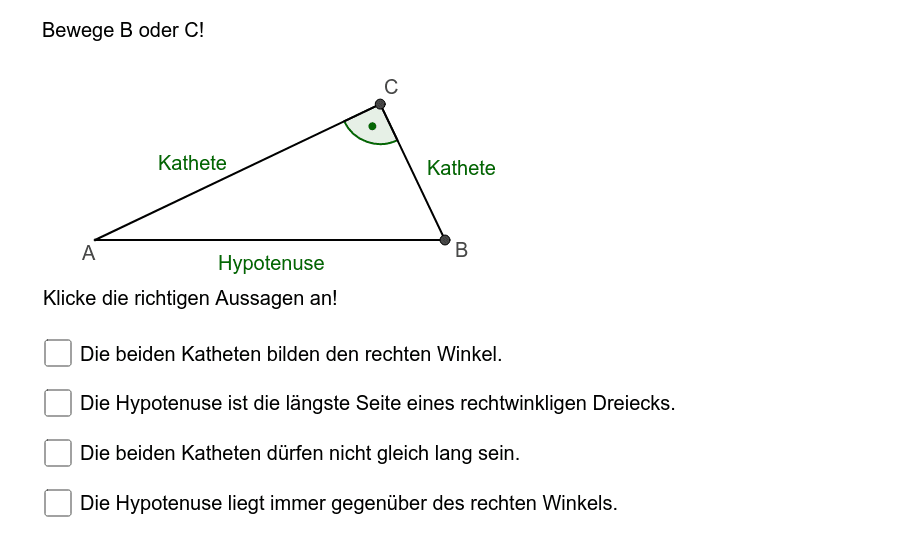
Das rechtwinklige Dreieck Grundbegriffe GeoGebra
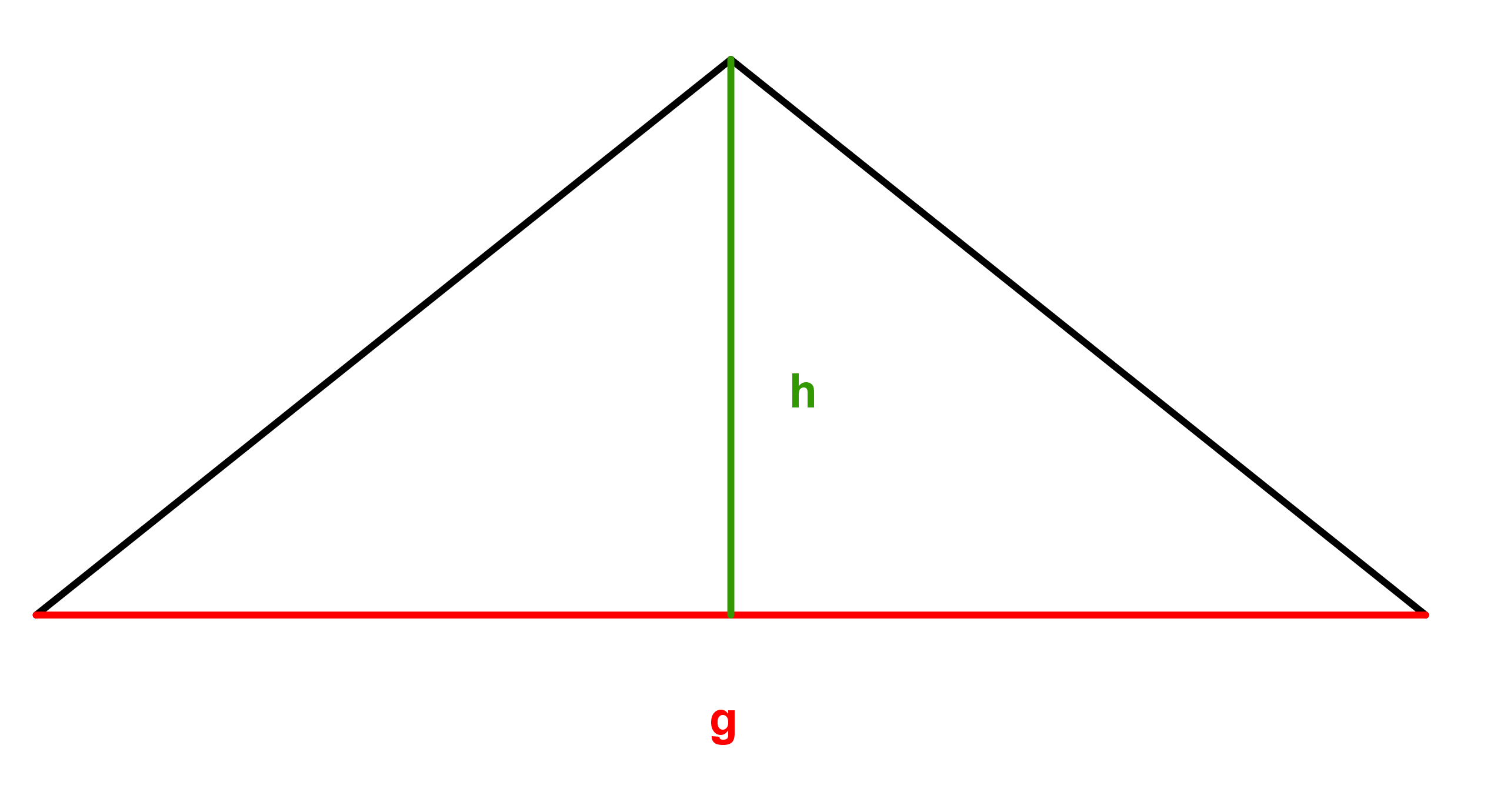
Aufgaben zur Flächenberechnung von Dreiecken lernen mit Serlo!
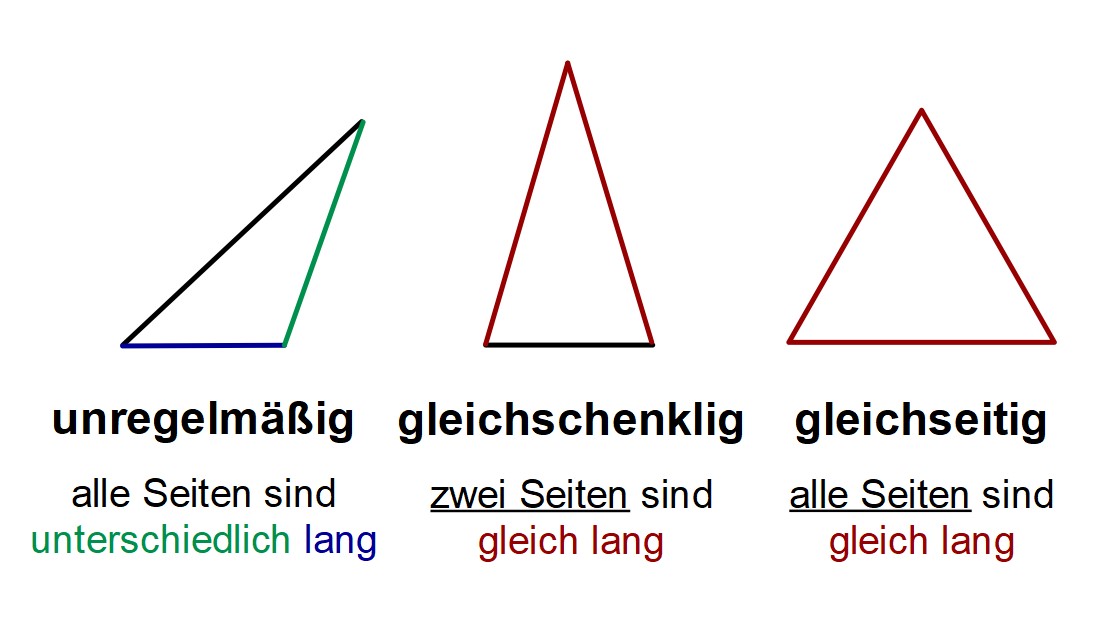
Dreiecke Klasse 7 Zusammenfassung
Innenwinkelsumme Dreieck • Erklärungen und Beispiele · [mit Video]
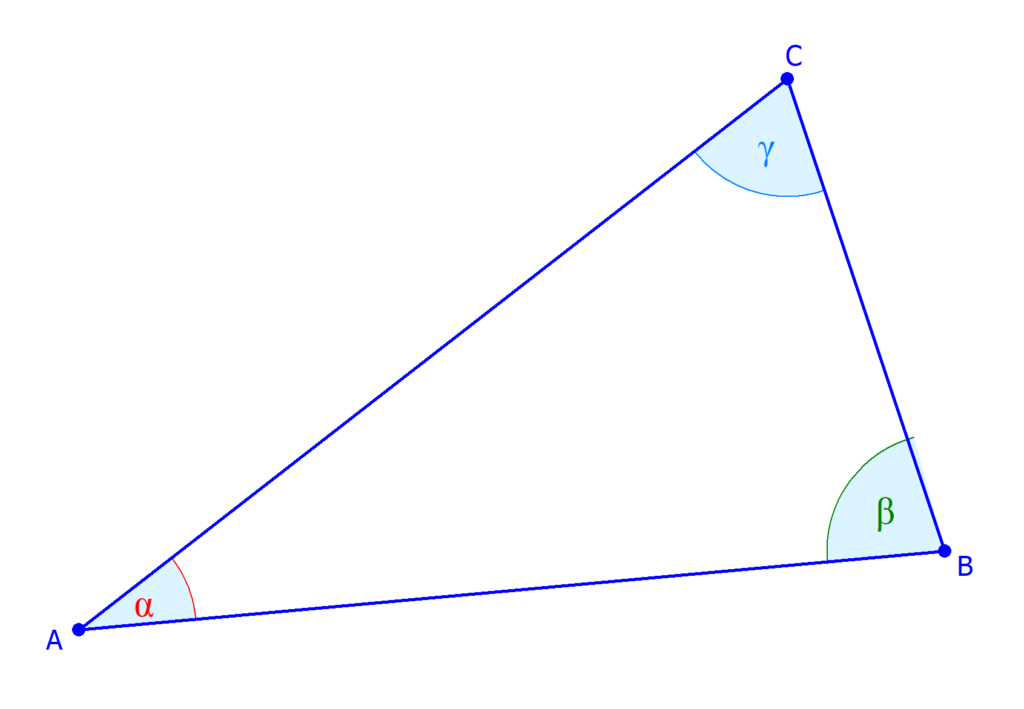
Innenwinkelsumme Dreieck • Erklärungen und Beispiele · [mit Video]
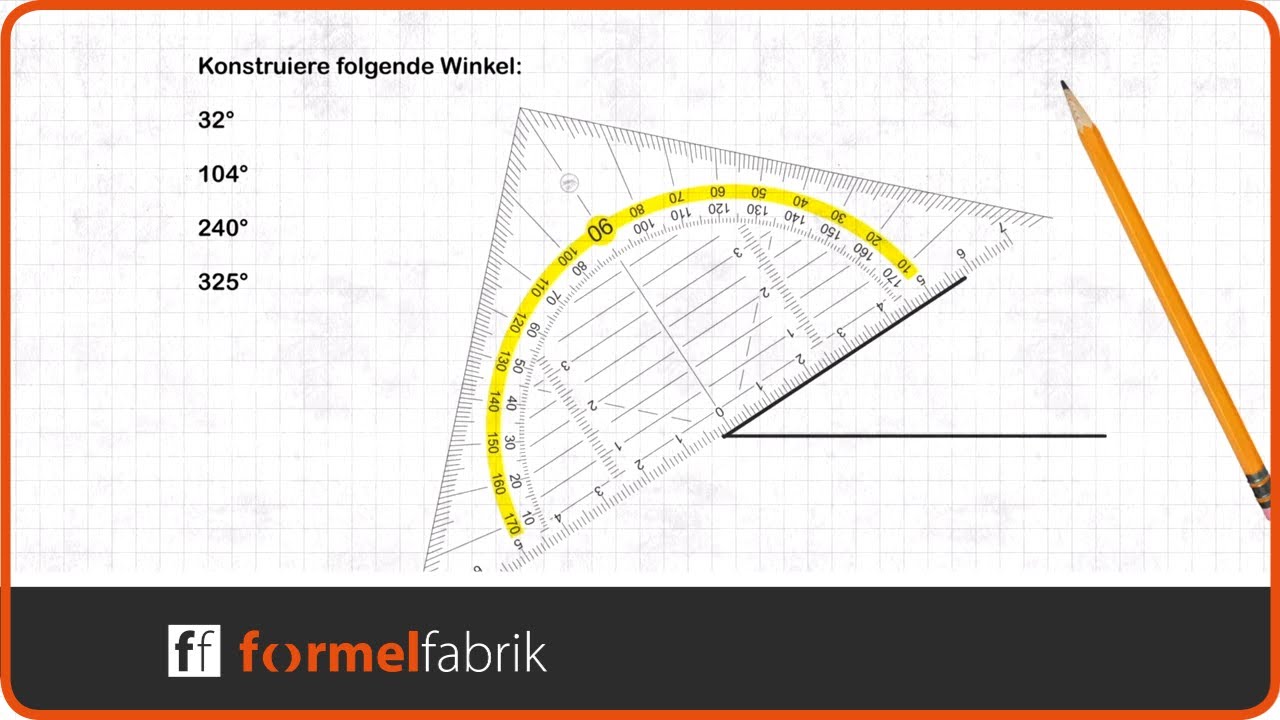
Winkel konstruieren mit dem Geodreieck SchrittfürSchrittAnleitung YouTube
Einführung SchulLV
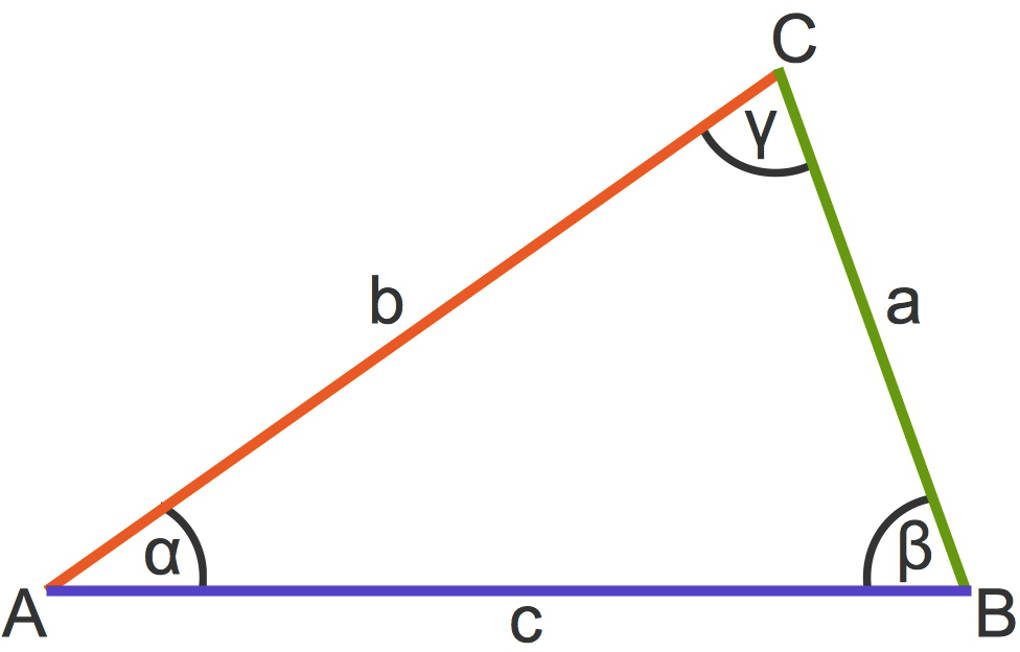
Winkel im Dreieck Mathematik SchuBu

Winkel im Dreieck YouTube
Online Rechner Trigonometrie OnlineBerechnungen am rechtwinkligen und am allgemeinen
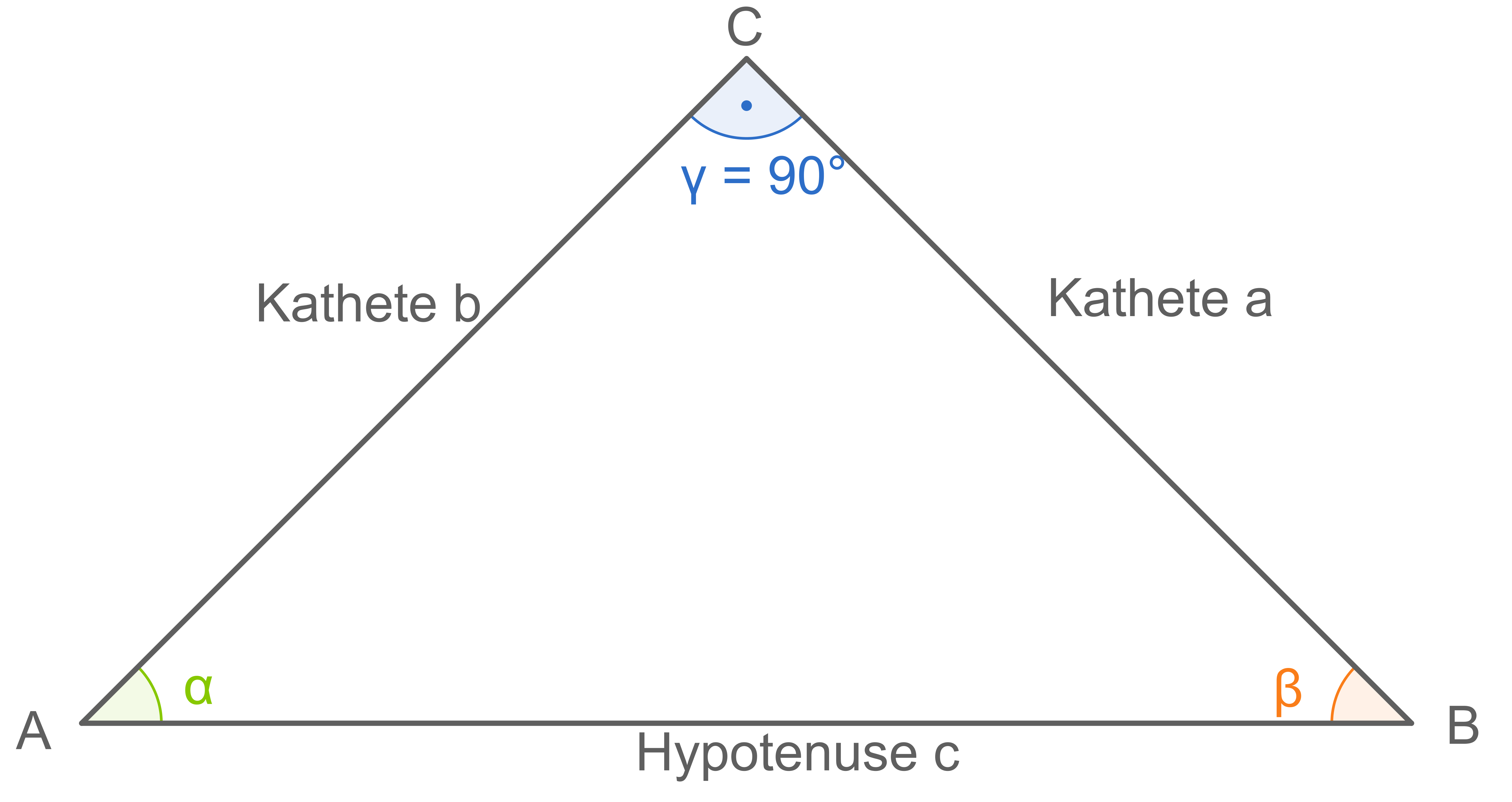
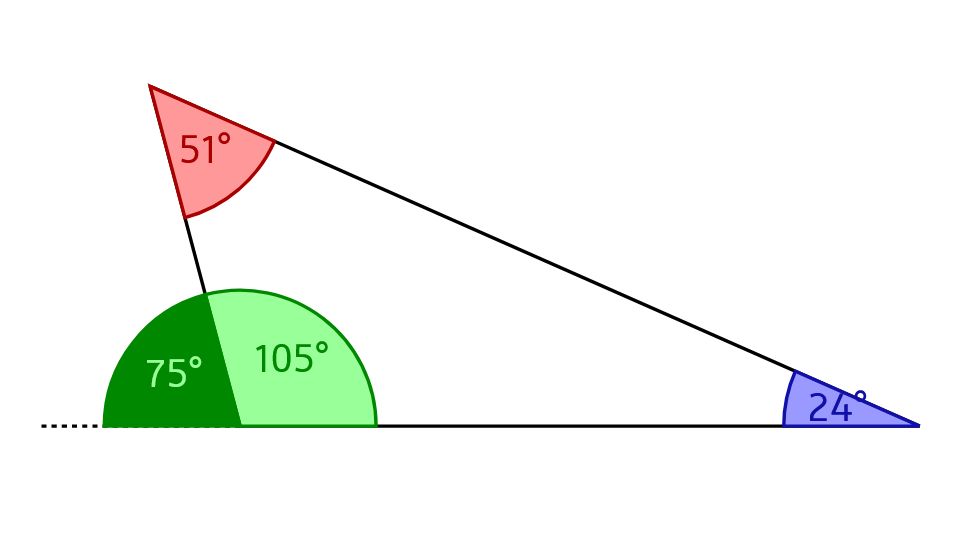
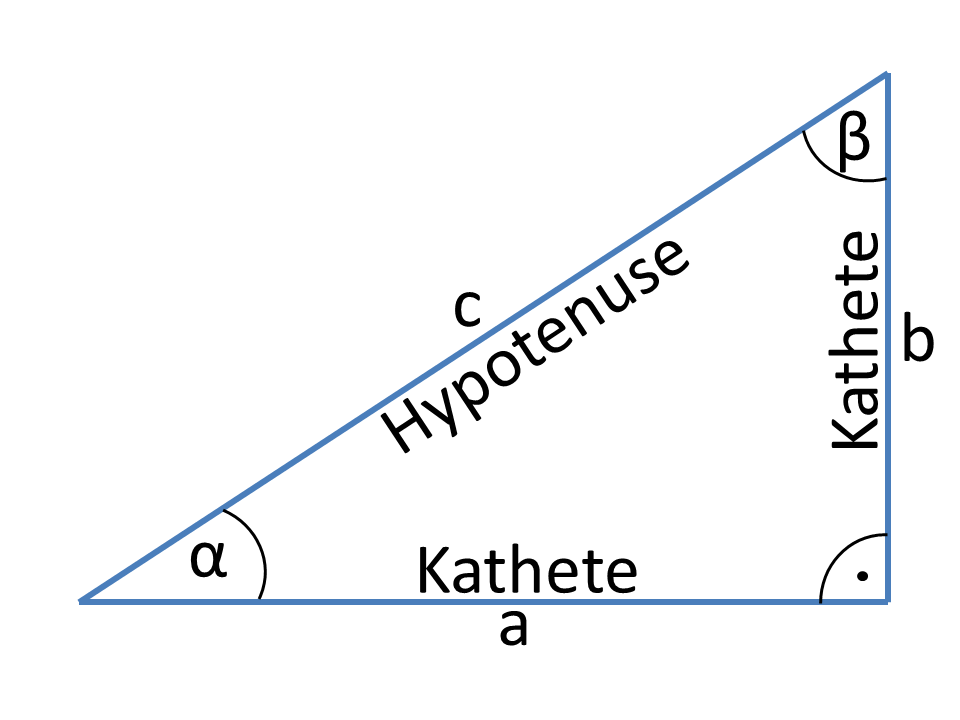
Rechtwinkliges Dreieck: Weist das Dreieck einen Innenwinkel von exakt 90 Grad auf ist es ein rechtwinkliges Dreieck. Spitzwinkliges Dreieck: Sind alle Winkel im Dreieck kleiner als 90 Grad handelt es sich um ein spitzwinkliges Dreieck. Innenwinkelsatz: Rechnet man die drei Winkel im Dreieck zusammen, erhält man immer 180 Grad.. In jedem Dreieck beträgt die Summe der Außenwinkel 360 ∘. Folglich gilt: α ′ + β ′ + γ ′ = 360 ∘. Herleitung. Außenwinkelsumme. Abb. 2 / Außenwinkelsumme. Vorheriges Kapitel Nächstes Kapitel. Über den Autor. Winkelsumme im Dreieck einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!


