ovvero la forma più comune per scrivere l’equazione di un fascio proprio di rette con centro nel punto di intersezione tra le due rette {r_1 : a_1x+b_1y+c_1} e {r_2:a_2x + b_2y+c_2}. Le rette {r_1} ed {r_2} si dicono rette generatrici del fascio. E la retta la cui equazione è moltiplicata per il parametro {k} si dice retta esclusa.. Un fascio di rette è un insieme di rette definito da un’equazione parametrica. Si distinguono due tipi di fasci di rette: proprio: è l’insieme delle infinite rette che intersecano un determinato punto nel piano cartesiano. improprio: è l’insieme delle infinite rette caratterizzate da uno stesso coefficiente angolare e quindi parallele tra di loro.

Centro Del Fascio Di Rette ataontell
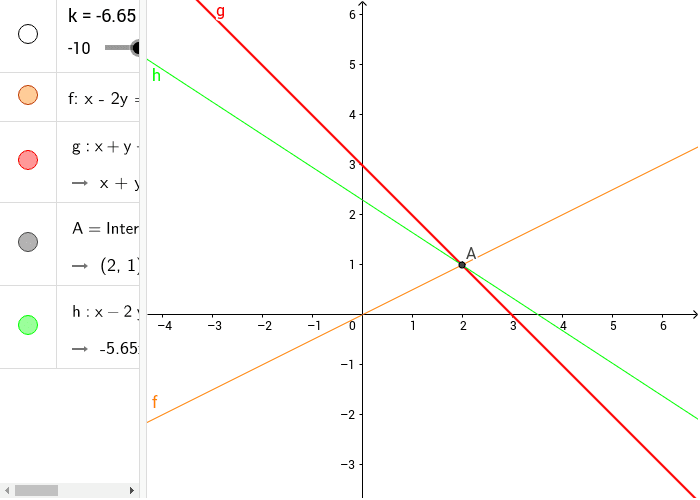
Fascio generato da due rette incidenti GeoGebra
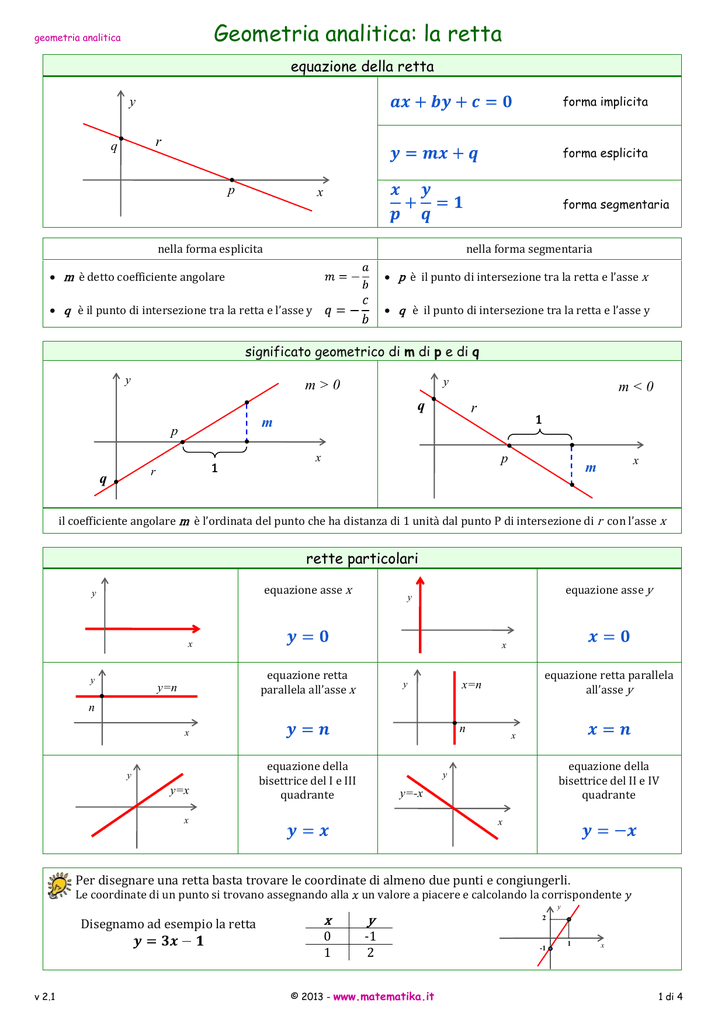
Scrivi L’equazione Della Retta Appartenente Al Fascio Proprio Di Rette Di Centro (1 1) magachary

Fasci di Rette YouTube

FASCI DI RETTE PROPRI E IMPROPRI lezioniignoranti

Fascio di rette FORMULE ed ESEMPI SPIEGATI MondoFisica
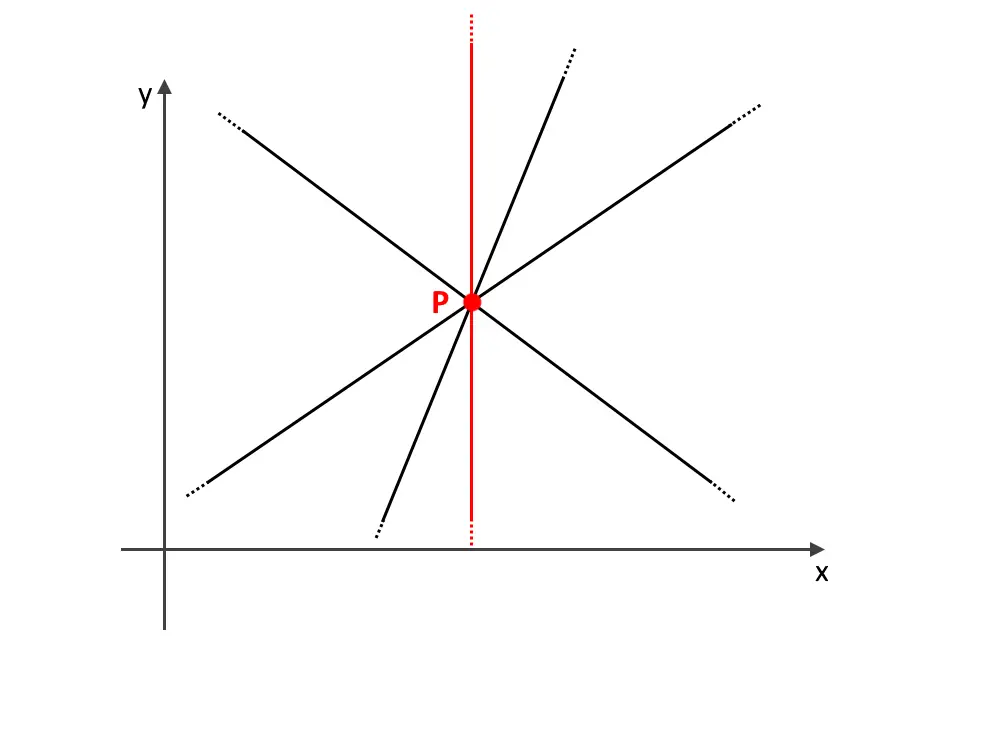
Fascio di rette FORMULE ed ESEMPI SPIEGATI MondoFisica

ESERCIZI SUI FASCI DI RETTE lezioniignoranti

FASCI DI RETTE PROPRI E IMPROPRI lezioniignoranti

Fascio Di Rette Esercizi Svolti broleesha

Centro Del Fascio Di Rette ataontell

Esempi di fasci di rette propri le equazioni da utilizzare

Retta R103 Piano cartesiano, Fascio di rette proprio e centro del fascio Romoletto Blog
fascio proprio di rette

PPT Quante rette passano per un punto A del piano? PowerPoint Presentation ID5296533

Fasci di rette_1 propri e impropri YouTube
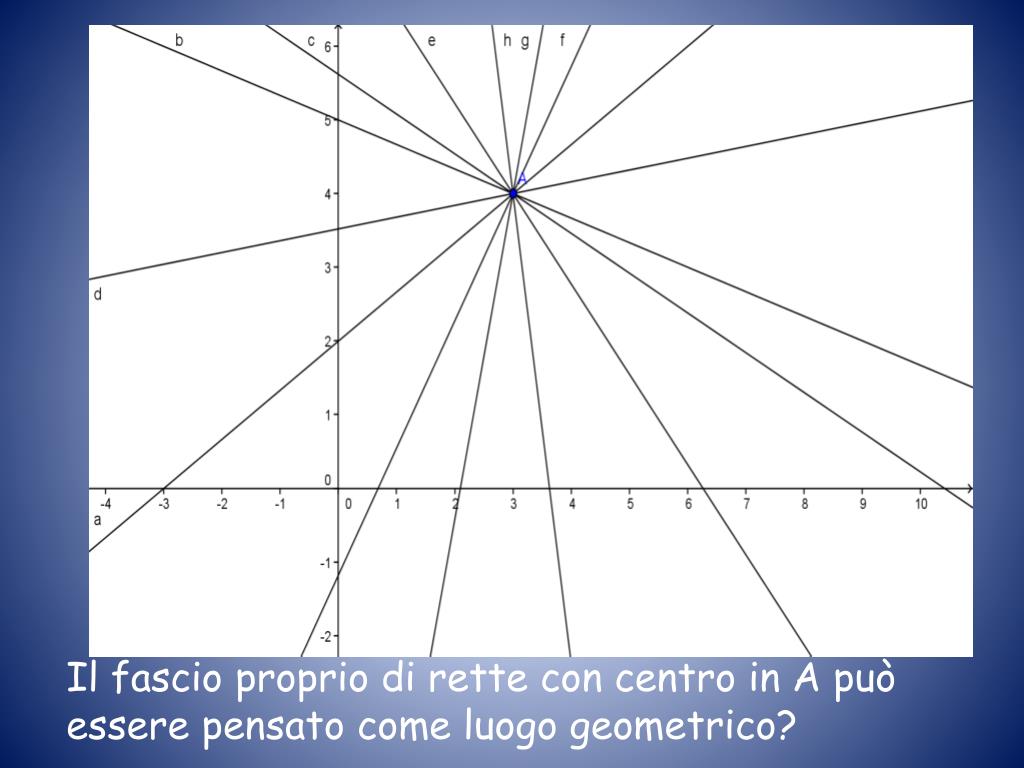
PPT Quante rette passano per un punto A del piano? PowerPoint Presentation ID5296533

PPT La retta PowerPoint Presentation, free download ID1975421

Fascio Proprio di Rette Caso 1 Centro Fascio su Asse y

Fascio di rette GeoGebra
Un fascio improprio di rette (o fascio di rette parallele) è un insieme di rette tutte parallele tra loro, che dunque non hanno alcun punto in comune, ed descritto dall’equazione y=mx+q (k). Proseguiamo lo studio dei fasci di rette e passiamo ad analizzare nel dettaglio il caso del fascio improprio di rette.. Il punto P comune a tutte le rette del fascio si chiama centro del fascio. ESEMPIO. Determiniamo l’equazione del fascio di rette di centro P (4;3). Se una retta generica y = m x + q deve passare per P, occorre che le coordinate di P soddisfino l’equazione, ossia: 3 = m • 4 + q. Ricaviamo q : q = 3 − m • 4.


